EXCELによる最長片道ルート探索
3. 簡単な計算例
以上の定式化が実際にどのように処理されるのかを図18の簡単な例で見てみることにする。

図18
ここで、接続駅はA〜Fの6駅、枝は(A,B)〜(D,F)の10区間である。この中で起終点が連結している一筆書きの最長ループを求めてみたい。
まず、目的関数を作るために全ての区間を左表の1列目(R9C2:R18C2)に列挙し、対応する距離を2列目(R9C3:R18C3)に記入する。3列目(R9C4:R18C4)は0又は1を取る変数H(a,b)とするので取り敢えず全て0を入れておき、4列目 (R9C5:R18C5)に2列目×3列目の式(=R9C3:R18C3*R9C4:R18C4)を入れる。すると4列目を縦に合計したセル(R19C5)が目的関数の値となる。次に制約式を設定する。まず、事前に左上の地図上の対応する区間に変数H(a,b)の値が表示されるよう式を入れておき(例えばH(A,B)ならR3C3に=R9C4を入力)、次に右表に接続駅毎にその地図上の数値を足し合わせる数式(例えばAならR9C8に=R3C3+R4C3+R5C3を入力)を入れて、接続駅毎に、その駅に接続しているH(a,b)の合計を表示させる。
次に「全ての接続駅において、ルートに含まれる枝は2本又は0本である」の制約はダミー変数による方法を使うことにする。即ち、接続駅毎のH(a,b)の合計値を入れた次の列に(変数H(a,b)の合計値)/2の値を表示するように式(例えばAならR9C9に=R9C8 / 2を入力)を入れ、一方で左表の下(R21C4:R26C4)にダミー変数を接続駅の数だけ追加しておく(ダミー変数は取り敢えず全て0としておく)。
ここまで準備したら、「ツール」から「ソルバー」を選択し、まず「目的セル」として「R19C5」、「目標値」として「最大値」、「変化させるセル」として「R9C4:R18C4, R21C4:R26C4」と入力する。次に「制約条件」の「追加」をクリックして制約式を入れていく。まず、「H(a,b)=0または1」は「R9C4:R18C4>=0、R9C4:R18C4<=1、R9C4:R18C4(区間)整数」と入力する。次に、「A、B、C、D、E、Fを通る枝はそれぞれ2本または0本」は「R9C8:R14C8<=2、R9C9:R14C9=R21C4:R26C4、R21C4:R26C4(区間)整数」と入力すればよい。
ここで、EXCELのソルバーは計算方法の初期設定が特殊であるため、オプションをクリックしてこれを若干変更する必要がある。変更が必要なのは「線形モデルで計算」を選択することと、公差5%となっているのを0%にすることである。「線形モデルで計算」を選択するのは非線型計算のままだと処理能力がかなり小さく、すぐエラーになってしまうからである。公差というのは次のようなものである。整数計画法は、分岐限定法という、場合によっては非常に時間の掛かる手法を採用しており、例えばパソコンに半日計算させても計算が終らないこともある。そこで、最適解に若干劣る解でも、条件を満たす整数解が最適解候補を列挙している途中で求まったら、それを解として採用し、以後の計算をしないで済ませることがある。公差というのはその許容誤差を表わしている。しかし、最長片道ルート問題では、最長であることだけに意味があり、0.1kmでも最長ルートより短ければ意味がないので、この公差を0%とする必要がある。
このようにして求めた結果が図18の状態である。最適解は74となるが、左上の地図で1と表示された区間を辿ると、一筆書きにはなっておらず、A−C−E−A、B−D−F−Bの2つの部分巡回ルートが形成されていることが分かる。
求めたルートが一筆書きにならなかったので、部分巡回ルートを解消する条件
H(A,B)+H(B,E)+H(D,E)+H(C,D)=>1
を追加する必要がある。そこで、R16C7に=R3C3+R3C4+R4C5+R5C5を入力し、ソルバーの制約条件にR16C7=>1を追加して再計算させることにする。

図19
再計算の結果が図19である。最適解は59であり、A−B−F−D−E−C−Aと片道ルートになっている。条件は全て満たされたのでこれが最長ルートである。なお、部分巡回ルートに関する制約を課さずにどちらかの部分ループを放棄することが最長となる可能性を排除する必要があるが、A−C−E−Aの部分ループの距離は35、B−D−F−Bの距離は39であり、どちらを削除するケースも59より小さいので、部分ループの放棄が最適値をもたらす可能性はないことが分かる。
ここで、EXCELで実際にどのように整数計画法が実行されたかを図20に記しておくことにする。以下の知識はなくても計算できるが、なぜ計算に時間が掛かるのかが理解できると思う。なお、これらの計算過程は、「ソルバー」「オプション」の「反復結果の表示」をクリックしてオンにすることで、一過程毎に一時停止させ、結果を確認することができる。
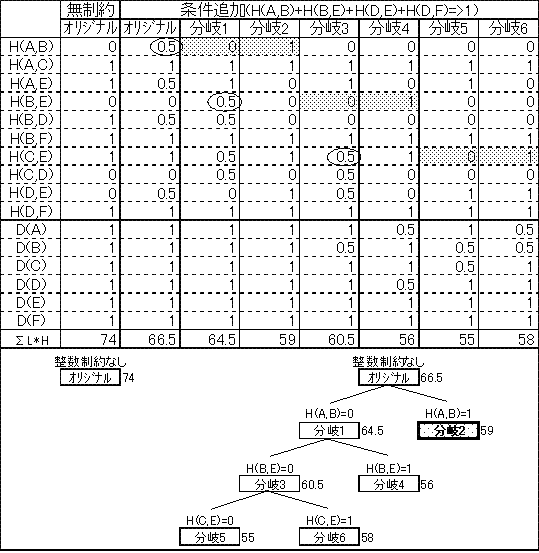
図20
整数計画法は、まず整数条件を外した線形計画問題を解き、H(a,b)が全て整数であったらそれを解とし、そうでない場合は整数にならないH(a,b)について、それを0とする制約を追加するケースとそれを1とする制約を追加するケースに分け(これを分岐と呼ぶ)、それぞれを再度、(整数条件を外した)線形計画問題として解く、という手順を繰り返して最適解を求めていく。
最左列の「無制約」というのは「部分巡回ルートに関する制約を課す前」という意味で、「オリジナル」というのは、「整数条件を取り外して求めた解」という意味である。この「無制約・オリジナル」はH(a,b)が全て整数になっているが、これは整数条件を取り外して計算しても偶々最適解が整数であったことを表わしている。その最適解が74である。
条件H(A,B)+H(B,E)+H(D,E)+H(C,D)=>1を加えると、今度は整数制約なしのオリジナルの解にH(A,B)=0.5、H(A,E)=0.5、H(B,D)=0.5、H(D,E)=0.5の小数解が含まれていることが分かる。従い、そこで分岐が行われ、まずH(A,B)=0の制約(分岐1)とH(A,B)=1の制約(分岐2)で再計算される。分岐1には4つの小数解が含まれるので再度分岐が必要になるが、分岐2は全て整数解となっている。従って、分岐2の解59が最適解の候補になる。分岐1は、現在小数解であるH(B,E)に対し、H(B,E)=0の制約(分岐3)とH(B,E)=1の制約(分岐4)を追加して再計算がされる。分岐3と分岐4はいずれも小数解を持つが、分岐4の解56は最適解候補分岐2の解59より小さいので、分岐4にこれ以上の制約を追加しても59より大きな解が求まることは有り得ない。従い、解が60.5で59より大きい分岐3のみが再度分岐される。この様に最適解を持つ可能性のない分岐を中断するのが分岐「限定」法の限定たる所以である。分岐3はH(B,E)で分岐5及び分岐6に分岐される。分岐5及び分岐6はいずれも小数解を持つが、分岐5の解は55、分岐6の解は58で、最適解候補分岐2の解59より小さいため、どちらもこれ以上の分岐は中止される。この時点で、全ての候補は調べ終わったことになり、分岐2が最適解であるという計算結果が出ることになる。
更新記録
・ 2005年6月21日 : 「部分巡回」「部分循環」を「部分巡回」に用語統一。
←前のページ 目次 次のページ→
Copyright(c) 2005 KONDO Hideaki All rights reserved.
初版: 2005年2月12日 最終更新: 2005年6月21日



