俤倃俠俤俴偵傛傞嵟挿曅摴儖乕僩扵嶕
4. 俰俼嵟挿曅摴儖乕僩偺寁嶼
乮侾乯怴姴慄傪娷傓捠忢偺嵟挿曅摴儖乕僩
師偵丄偙偺庤朄傪幚嵺偺俰俼嵟挿曅摴儖乕僩偺寁嶼偵揔梡偟偰傒傞丅埲壓偱偼杮廈偺傒傪庢傝埖偆丅
傑偢丄怴姴慄傪娷傓捠忢偺嵟挿曅摴儖乕僩傪媮傔傞偨傔丄婲揰傪杒奀摴傊偺擖岥偱偁傞惵怷丄廔揰傪嬨廈傊偺擖岥偱偁傞敠惗偲偡傞丅懄偪惵怷丄敠惗傪捠傞巬偺悢偼1偲偄偆惂栺傪壽偡偙偲偲偡傞丅傑偨帠慜偺張棟偲偟偰峴偒巭傑傝楬慄偼慡偰嶍彍偡傞偺偼栜榑偲偟偰丄搑拞偵暘婒揰傪娷傑側偄2抧揰娫傪寢傇儖乕僩偑暋悢偁傟偽丄嵟挿儖乕僩偺傒傪巆偟懠偼嶍彍偡傞偙偲偲偟偨丅偙傟偵傛傝丄惵怷丒廐揷娫偼屲擻慄宱桼偺傒丄惙壀丒怴壴姫娫偼嶳揷慄丄姌愇慄宱桼偺傒丄慼変丒戝栐娫偼撪朳慄亅埨朳姏愳亅奜朳慄宱桼偺傒丄墶昹丒戝慏娫偼崻娸慄宱桼偺傒丄憡惗丒搶壀嶳娫偼嶳梲杮慄宱桼偺傒丄暉嶳丒嶰尨娫偼嶳梲杮慄宱桼偺傒丄嶰尨丒峀搰娫偼屶慄宱桼偺傒丄峀搰丒怴嶳岥娫偼嶳梲杮慄宱桼偺傒丄傑偨怴嶳岥丒岤嫹娫偼嶳梲杮慄亅塅晹亅塅晹慄亅嫃擻亅彫栰揷慄宱桼偺傒偲側傞丅奺嬫娫偺嫍棧偲偟偰偼丄慡偰塩嬈僉儘傪嵦梡偟偨丅
偙偆偟偰杮廈慡偰偺嬫娫傪擖椡偟偰偄偔偲丄杒奀摴傗嬨廈偺嵟挿儖乕僩傪寁嶼偟偨帪偲摨偠傛偆偵丄儖乕僩偺慖戰巿偑2捠傝傗3捠傝偟偐側偄抧揰偱丄寁嶼傪暘妱偱偒偦偆側偙偲偑暘偐傞丅傑偢丄儖乕僩偺慖戰巿偑2捠傝偟偐側偄偺偼丄壛屆愳丒昉楬亅暉抦嶳丒榓揷嶳乮恾21乯偲丄怴嶳岥丒岤嫹亅塿揷丒挿栧巗偺2儠強偑尒偮偐傞丅
 丂
丂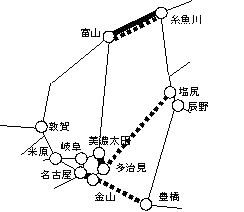
恾21丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恾22
椺偲偟偰恾21偱偺寁嶼暘妱偺曽朄傪峫偊傞丅傑偢丄嘆壛屆愳丒昉楬偺傒捠夁偡傞働乕僗丄嘇暉抦嶳丒榓揷嶳偺傒捠夁偡傞働乕僗丄嘊慡偰捠夁偡傞働乕僗偵暘偗傞丅偙偙偱丄捠忢偺曅摴嵟挿儖乕僩偼杒奀摴偐傜嬨廈傑偱堦杮摴偲側傞偙偲偐傜丄嘊偺働乕僗偑嵟挿儖乕僩偵側傞偙偲偼偁傝偊側偄偙偲偑暘偐傞丅偳偪傜偐偺儖乕僩偱堦搙惣傊岦偐偆偲丄嵞搙偦偙傪搶傊岦偐偆偵偼傕偆堦曽傪捠傜側偗傟偽側傜偢丄師偵惣傊岦偐偆嵺偺儖乕僩偑側偔側偭偰偟傑偆偐傜偱偁傞丅廬偭偰丄嘆嘇偺2働乕僗偵偮偄偰丄暘妱偟偨僄儕傾枅偵嵟挿儖乕僩傪嶼弌丄懌偟崌傢偣偨嫍棧偺挿偄曽偑嵟挿儖乕僩偲側傞丅
師偵丄儖乕僩偺慖戰巿偑3捠傝偟偐側偄偺偑丄晉嶳丒巺嫑愳亅旤擹懢揷丒懡帯尒亅嬥嶳丒柤屆壆乮恾22乯乮晉嶳丒巺嫑愳亅墫怟丒懡帯尒亅嬥嶳丒朙嫶偱傕壜乯丄嶁挰丒怴敪揷亅暉搰丒孲嶳亅偄傢偒丒娾徖丄堦僲娭丒杒忋亅怴彲丒墶庤亅梋栚丒廐揷偺3儢強偱偁傞丅
儖乕僩偺慖戰巿偑3捠傝偲側傞恾22偱傕摨條偵丄嘆晉嶳丒巺嫑愳偺傒捠夁偡傞働乕僗丄嘇旤擹懢揷丒懡帯尒偺傒捠夁偡傞働乕僗丄嘊嬥嶳丒柤屆壆偺傒捠夁偡傞働乕僗丄嘋晉嶳丒巺嫑愳偲旤擹懢揷丒懡帯尒偺傒捠夁偡傞働乕僗丄嘍晉嶳丒巺嫑愳偲嬥嶳丒柤屆壆偺傒捠夁偡傞働乕僗嘐旤擹懢揷丒懡帯尒偲嬥嶳丒柤屆壆偺傒捠夁偡傞働乕僗丄嘑慡偰捠夁偡傞働乕僗偵暘偗傞丅偙偙偱傕丄儖乕僩偺慖戰巿偑2捠傝偺応崌偲摨條偵丄3儖乕僩拞偺2儖乕僩捠夁偲側傞嘋嘍嘐偺働乕僗偑嵟挿儖乕僩偵側傞偙偲偼偁傝偊側偄偙偲偑暘偐傞丅偮傑傝幚嵺偵寁嶼偟側偗傟偽側傜側偄偺偼丄嘆嘇嘊嘑偺4捠傝偩偗偱偁傞丅
峏偵丄偙偙偱柺敀偄偙偲偑暘偐傞丅嘑偺働乕僗偼丄峴偭偰丄栠偭偰丄傕偆堦搙峴偔偲偄偆偙偲偑壜擻偱偁傞偺偱丄偁傝偆傞僷僞乕儞偱偼偁傞偑丄栠偭偰棃側偄儖乕僩偑嘆嘇嘊偺3捠傝偁傞偺偵懳偟丄栠偭偰棃傞儖乕僩偼嘑偺1捠傝偟偐側偄偐傜丄嬼乆偦傟偑嵟挿儖乕僩偲側傞妋棪偼戝嶨攃偵尵偭偰1/4掱搙偟偐側偄偲峫偊傜傟傞丅偪側傒偵丄儖乕僩偺慖戰巿偑4捠傝偁傞偲丄栠偭偰棃側偄儖乕僩偑4捠傝丄栠偭偰棃傞儖乕僩偑4捠傝偲側傝妋棪偼1/2偵媫忋徃偡傞丅
偮傑傝丄嵟挿曅摴儖乕僩偑梤挵偨傞儖乕僩傪庢傞孹岦偑偁傞偲偄偭偰傕丄帠幚忋丄儖乕僩偺慖戰巿偑2丄3捠傝偺嬫娫偵暘抐偝傟偰偍傝丄偦偺娫傪屪偄偱峴偭偨傝棃偨傝偡傞偙偲偼杦偳側偄偲峫偊傜傟傞偺偱偁傞丅
椺偊偽丄媨榚弐嶰偺嵟挿曅摴愗晞偺椃偱偼丄乽朙嫶偐傜夛捗庒徏傑偱堷曉偡丄偲偄偆巹偺巚偄媦偽側偐偭偨儖乕僩偑偦偙偵帵偝傟偰偄偨丅乮拞棯乯栚揑抧偺枍嶈偵攚傪岦偗偰擇擔娫忔傝偮偯偗傞偺偩偐傜丄嵟挿曅摴愗晞側傜偱偼偩丅偟偐偟垻曫傜偟偝傕偙偙傑偱偔傞偲丄偐偊偭偰尩弆側庯傪掓偟偰偔傞偐偵巹偼巚偆偺偩偑丅乿偲弎傋偰偄傞偑丄椙偔尒傞偲乽朙嫶偐傜夛捗庒徏乿偺嬫娫偼晉嶳丒巺嫑愳亅旤擹懢揷丒懡帯尒亅嬥嶳丒柤屆壆乮晉嶳丒巺嫑愳亅墫怟丒懡帯尒亅嬥嶳丒朙嫶偱傕壜乯偲丄嶁挰丒怴敪揷亅暉搰丒孲嶳亅偄傢偒丒娾徖偱嬫愗傜傟偨嬫堟偺拞偩偗傪巊偭偨儖乕僩慖戰偱偁傝丄偦偺嬫堟偐傜偼堦搙傕堩扙偟偰偄側偄偙偲偑暘偐傞丅堦墳棟榑揑偵偼偙偺嬫堟傪弌擖傝偡傞嘑偺働乕僗傕峫偊傜傟傞偺偱偁傞偐傜丄朙嫶偐傜夛捗庒徏傑偱堷曉偡偲偄偆儖乕僩偼偦傟傎偳嬃偔偵抣偟側偄偺偐傕偟傟側偄丅
偝偰丄妺惣巵偼崅惈擻側僜儖僶乕傪巊梡偟偰偄傞偺偱丄擔杮慡崙傪慡偰揨傔偰寁嶼偟偰偄傞偑丄俤倃俠俤俴偺僜儖僶乕偼杮廈慡嬫娫傪堦搙偵寁嶼偟傛偆偲偡傞偲曄悢偑懡偡偓偰僄儔乕偑弌偰偟傑偆丅偦偙偱丄忋婰偺嬫暘傪棙梡偟偰寁嶼傪暘妱偡傞偙偲傪峫偊傞丅
傑偢丄儖乕僩偺慖戰巿偑2捠傝偟偐側偄抧揰偱暘妱傪峴偄僽儘僢僋枅偵寁嶼傪峴偆偙偲傪峫偊偨偑丄壛屆愳丒昉楬亅暉抦嶳丒榓揷傛傝搶懁偑曄悢偑懡偡偓偰僄儔乕偲側偭偰偟傑偭偨丅師偵儖乕僩偺慖戰巿偑3捠傝偟偐側偄抧揰偱暘妱傪峴偄僽儘僢僋枅偵寁嶼傪峴偆偲丄嵟傕僽儘僢僋偑戝偒偔側傞丄娭搶傪娷傓晹暘偑丄1夞偺寁嶼偱嵟戝20暘掱搙帪娫偑妡偐傞傕偺偺丄側傫偲偐寁嶼傪幚巤偡傞偙偲偑偱偒偨丅
暘妱偼丄嶁挰丒怴敪揷亅暉搰丒孲嶳亅偄傢偒丒娾徖傛傝杒傪搶杒抧曽乮搶杒抧曽偼彫偝偄偺偱丄堦僲娭丒杒忋亅怴彲丒墶庤亅梋栚丒廐揷偱暘妱偟側偔偰傕揨傔偰寁嶼壜擻偱偁偭偨乯丄晉嶳丒巺嫑愳亅旤擹懢揷丒懡帯尒亅嬥嶳丒柤屆壆傛傝惣傪惣擔杮抧曽丄偦偺娫傪搶擔杮抧曽偲偟丄愙懕晹偺嬫娫偼慡偰搶擔杮抧曽偵娷傔偰寁嶼偡傞偙偲偵偟偨丅
傑偢丄搶杒抧曽偼嶁挰丒怴敪揷亅暉搰丒孲嶳亅偄傢偒丒娾徖偑搶擔杮抧曽偲偺愙懕晹偲側傞偨傔丄師偺4働乕僗偵偮偄偰偦傟偧傟嵟戝抣傪媮傔傞丅
| 俫乮嶁挰丒怴敪揷乯 | 俫乮暉搰丒孲嶳乯 | 俫乮偄傢偒丒娾徖乯 | 嵟戝抣 | 儖乕僩 |
|---|
| 働乕僗嘆 | 1 | 0 | 0 | 1316.9 | 恾23
嶲徠 |
| 働乕僗嘇 | 0 | 1 | 0 | 1430.0 |
| 働乕僗嘊 | 0 | 0 | 1 | 1491.4 |
| 働乕僗嘋 | 1 | 1 | 1 | 1369.0 |
師偵丄惣擔杮抧曽偵偮偄偰傕丄搶擔杮抧曽偲偺愙懕晹傪忋婰偲摨條偵師偺4働乕僗偵暘偗丄偦傟偧傟嵟戝抣傪媮傔傞丅
| 俫乮晉嶳丒巺嫑愳乯 | 俫乮旤擹懢揷
丂丒懡帯尒乯 | 俫乮嬥嶳丒柤屆壆乯 | 嵟戝抣 | 儖乕僩 |
|---|
| 働乕僗嘆 | 1 | 0 | 0 | 3202.5 | 恾24
嶲徠 |
| 働乕僗嘇 | 0 | 1 | 0 | 3283.1 |
| 働乕僗嘊 | 0 | 0 | 1 | 3329.6 |
| 働乕僗嘋 | 1 | 1 | 1 | 3131.1 |
嵟屻偵搶擔杮抧曽偵偮偄偰偼丄搶杒抧曽偲偺愙懕偺慻傒崌傢偣4捠傝亊惣擔杮抧曽偲偺愙懕偺慻傒崌傢偣4捠傝亖16捠傝偺慻傒崌傢偣傪寁嶼偡傞昁梫偑偁傞丅
| 惣擔杮抧曽 |
搶
杒
抧
曽 |
働乕僗柤
嵟戝抣
乮巄掕嵟戝抣岓曗偲偺嵎乯 |
働乕僗嘆 | 働乕僗嘇 | 働乕僗嘊 | 働乕僗嘋 |
3202.5
(-127.1) | 3283.1
( -46.5) | 3329.6
( 0.0) | 3131.1
(-198.5) |
| 働乕僗嘆 | 1316.9
(-174.5) | 仜 | 仜 | 仜 | 仜 |
| 働乕僗嘇 | 1430.0
( -61.4) | 仜 | 仜 | 仜 | 仜 |
| 働乕僗嘊 | 1491.4
( 0.0) | 仜 | 仜 | 3533.6 | 仜 |
| 働乕僗嘋 | 1369.0
(-122.4) | 仜 | 仜 | 3572.5
埲壓 | 仜 |
偙偙偱丄16捠傝慡偰偺嵟戝抣傪媮傔傞偺偼庤娫偑妡偐傞偨傔丄埲壓偺傛偆偵娙棯壔偟丄寁嶼夞悢傪嶍尭偡傞丅
傑偢丄搶杒抧曽偺嵟戝抣偲側傞働乕僗嘊偲惣擔杮抧曽偺嵟戝抣偲側傞働乕僗嘊偺慻傒崌傢偣偱搶擔杮抧曽偺嵟戝抣傪媮傔傞丅偙傟偑巄掕揑側慡懱嵟戝抣偺岓曗偲側傞丅偙傟偑杮摉偵嵟戝抣偱偁傟偽丄懠偺慻傒崌傢偣偼丄嵟戝抣傪寁嶼偡傞搑拞偱丄偙偺抣傛傝彫偝偔側傞偼偢偱偁傞丅椺偊偽丄搶杒抧曽偺働乕僗嘇偲惣擔杮抧曽偺働乕僗嘇偺慻傒崌傢偣傪峫偊傞応崌丄悘帪丄晹暘弰夞嬛巭惂栺傪捛壛偟偰偄偔夁掱偱丄巄掕揑側慡懱嵟戝抣偺岓曗偱偁傞3533.6偲斾妑偟偨嵎偑107.9(=搶杒抧曽61.4+惣擔杮抧曽46.5)傛傝傕彫偝偔側偭偨傜丄懄偪丄3641.5 (=3533.6+107.9)傛傝彫偝偔側偭偨帪揰偱丄偙偺働乕僗偼慡懱偱尰嵼偺岓曗抣傛傝傕彫偝偔側傞偙偲偑妋掕偡傞偨傔丄晹暘弰夞儖乕僩傪巆偟偨傑傑丄寁嶼傪拞抐偱偒傞偙偲偑暘偐傞偩傠偆丅
師偵丄愙懕晹傪傂偲偮傂偲偮摿掕偟偰寁嶼偡傞慜偵丄愙懕晹偺巬悢偵傛偭偰16働乕僗傪壓昞偺傛偆偵4偮偺斖埻偵暘偗丄偦傟偧傟偺嵟戝抣傪寁嶼偟偰丄偝傜偵屄暿寁嶼偡傞昁梫偺偁傞斖埻傪峣傝崬傓偙偲傪峫偊傞丅壓昞偼晹暘弰夞嬛巭惂栺偺側偄柍惂栺嵟戝抣傪寁嶼偟偨寢壥偱偁傞丅偙傟偵傛傝忋昞偺仜晹暘偼屄暿寁嶼晄梫偱偁傞偙偲偑暘偐傞丅
愙懕晹偺巬悢
(搶杒丄惣擔杮) | (1,1) | (1,3) | (3,1) | (3,3) |
奩摉働乕僗
(搶杒丄惣擔杮) | 塃婰埲奜
乮9拱絹j | (嘆,嘋) (嘇,嘋)
(嘊,嘋) | (嘋,嘆) (嘋,嘇)
(嘋,嘊) | (嘋,嘋) |
嵟戝抣
(3533.6偲偺嵎) | 3567.4
埲壓
(33.8) | 3552.5
埲壓
(18.9) | 3660.2
埲壓
(126.6) | 3635.1
埲壓
(101.5) |
寢嬊丄巆偭偨偺偼搶杒抧曽働乕僗嘋丄惣擔杮抧曽働乕僗嘊偺慻崌偣偺傒偱偁傞丅偙偺慻崌偣偵偮偄偰屄暿寁嶼傪峴偆丅偡傞偲丄娾徖亅暉搰亅孲嶳亅偄傢偒亅娾徖偺晹暘弰夞儖乕僩傪嬛巭偡傞惂栺幃俫乮孲嶳,偄傢偒乯亖0傪擖傟傞偙偲偱抣偑3572.5傑偱尭彮偟偨丅偙偙偱丄3572.5亙3533.6亄122.4偱偁傞偙偲偐傜丄偙偺働乕僗偼巄掕嵟戝抣岓曗傛傝彫偝偔側傞偙偲偑暘偐傞丅偨偩偟丄偙偺晹暘弰夞儖乕僩偼丄搶擔杮抧曽懁偱嬛巭偡傞偺偱偼側偔丄搶杒抧曽懁偱嬛巭偡傞偙偲傕峫偊傜傟傞丅偦偙偱丄搶杒抧曽偺嵟戝抣傪俫乮暉搰,娾徖乯亖0偺惂栺傪捛壛偟偰嵞寁嶼偟偰傒傞偲1318.0偲側偭偨丅偙傟偼丄僆儕僕僫儖偺1491.4偐傜173.4傕尭彮偟偰偄傞丅愙懕晹偺巬悢乮3,1乯偺嵟戝抣3660.2亙3533.6亄173.4傛傝丄傗偼傝巄掕嵟戝抣岓曗傛傝彫偝偔側傞偙偲偑暘偐傞丅
埲忋偵傛傝丄搶杒抧曽働乕僗嘊丄惣擔杮抧曽働乕僗嘊偲偟偨儖乕僩偑嵟挿曅摴儖乕僩偱偁傞偙偲偑帵偝傟偨丅偙偺応崌偺搶擔杮嵟挿曅摴儖乕僩傪恾25偵帵偟偰偍偔丅

恾23
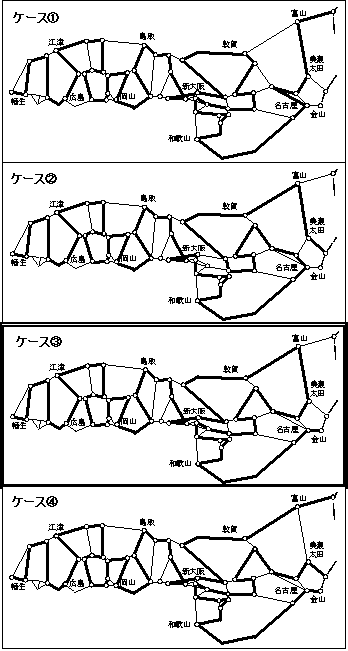
恾24
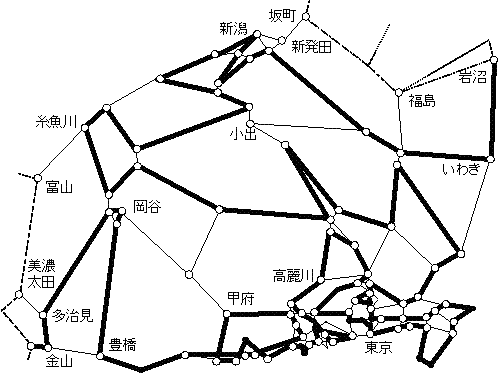
恾25
峏怴婰榐
- 2005擭7寧17擔
俤倃俠俤俴儚乕僋僔乕僩偵偮偒丄壓婰偺僨乕僞掶惓傪峴偄丄嵞寁嶼偟偨乮愳岥巵偺巜揈偵傛傞乯丅嵞寁嶼偵傛傝嫍棧偼曄峏偲側偭偨偑丄儖乕僩偼曄峏側偐偭偨丅
丂* 朙嫶-扖栰丂195.8km仺195.7km(2001擭4寧1擔丗揤棾愳帯悈岺帠偵娭楢偡傞愳楬墂堏愝偺斀塮楻傟)
丂* 晉嶳-撝夑丂190.2km仺190.1km(2002擭10寧21擔丗杒棨怴姴慄寶愝偵敽偆搶嬥戲墂堏愝偺斀塮楻傟)
丂* 捁庢-攲闼戝嶳丂88.0km仺87.9km(岆婰廋惓)
丂* 峀搰-怴嶳岥丂91.4km仺154.5km(岆婰廋惓)
側偍丄嵞寁嶼偵摉偨傝丄擔曢棦亅旜媣亅愒塇偲昳愳亅惣戝堜亅掃尒傪摿掕塣捓寁嶼僉儘偐傜塩嬈僉儘偵抲偒姺偊偨丅
仼慜偺儁乕僕丂栚師丂師偺儁乕僕仺
Copyright(c) 2005丂KONDO Hideaki丂All rights reserved.
弶斉丗 2005擭2寧12擔丂嵟廔峏怴丗 2005擭7寧17擔
 丂
丂
 丂
丂


