ＥＸＣＥＬによる最長片道ルート探索：東京メトロ編

4.最低運賃区間行列の作成

3章（2）の行列Zは、横に起点駅、縦に終点駅を並べ、最低運賃区間内であれば交点に1、そうでなければ0を入力した行列になっているが、107行107列となるので、要素が1万個以上となってしまう。これを手入力するのは非常に時間がかかり大変である。そこで、この行列の簡単な作成方法を示すことにする。

この行列Z作成でまず必要なことは、各駅間の最短距離をなるべく簡単に求めることである。そこで、インターネットで「最短経路問題」を検索したところ、「ウォーシャル・フロイド法」なる多点間の最短距離行列を求める手法があることが分かったので、これを活用することにした。この方法は、仕組みは簡単で、計算方法は次の通りであるが、この計算方法を思いついた人は天才的であると思う。この方法なら手入力と比べ所要時間は1/100以下にはなっているはずである。

枝1本だけ使う場合の最短距離の行列（枝1本だけで繋がらない区間は適当に大きな距離を入れておく）をつくる。
枝2本を使う場合の最短距離を計算し、もし枝1本だけ使う場合より短くなっていたら先の行列の数値をこれに置き換える。
この更新行列の中の、枝2本を使う場合の最短距離を計算して、行列を再更新すると、枝4本以下を使う場合の最短距離行列となる。
これを8回繰り返すと2⁸＝256の枝を使う場合が網羅される。（今回の枝の数は130しかないので、全部の枝を使うケース（ありえないが。）も網羅される。）

この方法で求めた最短距離の行列に対して、IF関数を用い、6km以下なら1、それ以外なら0という行列を作成するとそれが行列Zとなる。

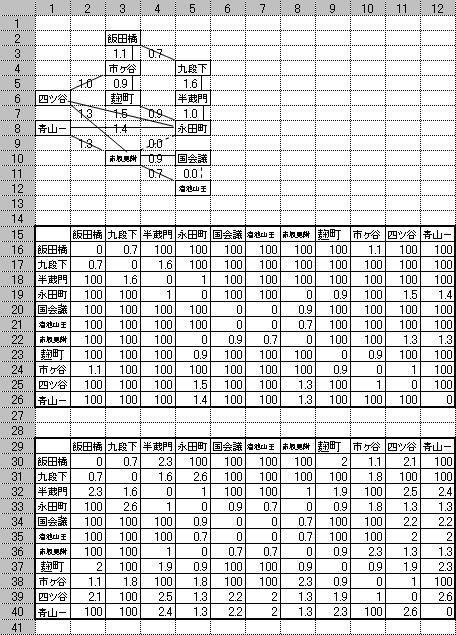
ここで、「ウォーシャル・フロイド法」の実際の手続きを、次の11行11列のケースで見てみることにする。

図M3

図M3
図M3は繰り返し計算前の状態である。まず、上の行列に各駅間の距離を入力する。繋がっていない駅間は100と入力している。これが1.の作業である。

次に下の行列の要素のどれか一つ、例えば(半蔵門,飯田橋)に

｛＝MIN(R2$C16:R3$C26＋TRANSPOSE($R2C18:$R12C18))｝

（注：{ }は行列を表わす。Ctrl+Shiftを押したままEnterを押すと単なる数値ではなく、行列として扱われ、自動的に{ }で囲まれる。）を入力し、これを他の全ての要素にコピーする。これが2.の作業である。(半蔵門,飯田橋)に入力した式は、飯田橋から半蔵門への距離を、他の駅を一駅だけ経由する全てのパターン（飯田橋→九段下→半蔵門、飯田橋→半蔵門→半蔵門、飯田橋→永田町→半蔵門、…、飯田橋→青山一丁目→半蔵門）の中のから最短のものに置き換える式となっているため、上の行列での数値100が下の行列では2.3に置き換わっていることが分かる。

3.の作業は、下の行列をコピーして、上の行列に、「形式を選択して貼り付け」を用いて、「値」を貼り付けるだけである。これで、上の行列が枝2本以下を使う場合の最短距離行列となるので、式の入った下の行列は自動的に枝4本以下を使う場合の最短距離行列になっているのである。

この時点で、下の行列はコピーを表す点線が点滅しており、コピーされた上の行列は色が反転しているはずである。ここで、色が反転している上の行列に再度、「形式を選択して貼り付け」を用いて、「値」を貼り付ける作業を行うと、上の行列は枝4本以下、下の行列は枝8本以下の最短距離行列に更新される。

この路線図は15本で構成されているため、この「形式を選択して貼り付け」を用いて、「値」を貼り付ける作業をあと2回繰り返せば、上の行列が枝16本以下の最短距離行列となるので、4.の作業が完了することになる。完了時の上の行列を図4に示す。

図M4

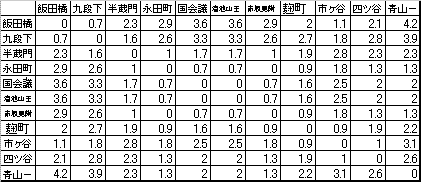
図M4

←前のページ　目次　次のページ→