俤倃俠俤俴偵傛傞嵟挿曅摴儖乕僩扵嶕
1.丂弰夞僙乕儖僗儅儞栤戣
嵟挿曅摴儖乕僩栤戣偼悽娫偱峀偔尋媶偼偝傟偰偄側偄偑丄偦傟偲嫟捠揰傪帩偭偰偄傞弰夞僙乕儖僗儅儞栤戣偼悽奅拞偱尋媶偝傟偰偍傝丄娭楢偡傞恾彂偑偨偔偝傫偁傞丅弰夞僙乕儖僗儅儞栤戣偑偙傟傎偳尋媶偝傟偰偄傞偺偼丄偦偺栤戣愝掕偺扨弮偝偵懳偟偰丄姰慡側夝朄偑側偔丄備偊偵夝朄偵岺晇偺梋抧偑懡偄偐傜偱偁傞丅
栤戣愝掕偼丄乽寛傔傜傟偨暋悢偺搒巗傪堦昅彂偒偱弰夞偡傞嵟抁宱楬傪媮傔傛乿偲偄偆傕偺偱偁傞丅
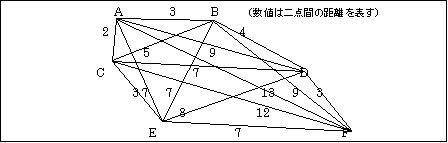
恾15
椺偊偽丄恾15偺俙乣俥偺6搒巗傪堦昅彂偒偱弰夞偡傞嵟抁宱楬傪峫偊偰傒傞丅偙偺応崌丄搒巗傪寢傇巬偼6C2=15杮偱偁傝丄6搒巗傪弰夞偡傞偨傔偵偼偦偺巬偐傜6杮傪慖戰偡傞昁梫偑偁傞偺偱丄偦偺慻傒崌傢偣偼15C6=5005捠傝偁傞偙偲偵側傞丅偙偺栤戣偺堦斣扨弮側夝朄偼丄偙偺5005捠傝偺拞偐傜弰夞儖乕僩偵側偭偰偄傞傕偺傪慖傃弌偟丄偦偺嫍棧傪慡偰寁嶼偟偰丄嵟抁偺傕偺傪媮傔傞偙偲偱偁傞丅偟偐偟丄偙偺傛偆側扨弮楍嫇朄偼搒巗悢偑憹壛偡傞偲慻崌傢偣敋敪傪婲偙偟偰捈偖偵攋抅偡傞偙偲偵側傞丅搒巗悢100偺応崌丄100C2=4950丄4950C100=1.1305亊10211偲側傞偑丄1.1305亊10211捠傝傪慡偰寁嶼偡傞偵偼1020夞/昩乮偪側傒偵3GHz 32bit 俠俹倀偺摦嶌夞悢偼栺1.3亊1019夞/昩乯偺懍搙偱寁嶼偟偰傕丄10183擭乮偪側傒偵抧媴偺擭楊偼栺40壄擭亖4亊109擭乯埲忋偐偐傞寁嶼検側偺偱偁傞丅
偦偙偱丄敪憐傪曄偊偰丄偙傟傪俤倃俠俤俴偺僜儖僶乕側偳偵傛傝娙扨偵夝傪媮傔傞偙偲偑偱偒傞惍悢寁夋栤戣偵帩偪崬傓偙偲偑丄弰夞僙乕儖僗儅儞栤戣偺嵟揔夝傪媮傔傞嵺偺1偮偺傾僀僨傿傾偱偁傞丅
偙傟傪惍悢寁夋栤戣偵偡傞偨傔偵丄傑偢丄搒巗a丄搒巗b傪寢傇巬偵懳偟偰丄偦偺巬傪捠傞応崌偼1丄捠傜側偄応崌偼0傪庢傞曄悢H乮a,b乯傪愝掕偟丄
T = 3H(A,B)+2H(A,C)+9H(A,D)+7H(A,E)+13H(A,F)+5H(B,C)+4H(B,D)+7H(B,E)+9H(B,F)+7H(C,D)+3H(C,E)+12H(C,F)+8H(D,E)+3H(D,F)+7 H(E,F)
傪嵟彫壔偡傞偙偲傪峫偊傞丅椺偊偽丄俙仺俛仺俠仺俢仺俤仺俥仺俙偺弴斣偵夞傞偲H(A,B)丄 H(B,C)丄H(C,D)丄H(D,E)丄H(E,F)丄H(A,F)偑1偲側傝丄偦傟埲奜偺H(a,b)偼0偲側傞偐傜丄T亖3亊1+2亊0+9亊0+7亊0+13亊1+5亊1+4亊0+7亊0+9亊0+7亊1+3亊0+12亊0+8亊1+3亊0+7亊1亖43偱偁傞丅
偙偺T傪乽堦昅彂偒乿偲偄偆忦審偺壓偱嵟彫壔偡傟偽椙偄丅栤戣偼丄偙偺乽堦昅彂偒乿偲偄偆忦審傪掕幃壔偡傞偙偲偱偁傝丄惍悢寁夋栤戣偵偡傞偨傔偵偼偙傟傪慄宍惂栺幃偵偡傞昁梫偑偁傞偺偱偁傞丅
弰夞僙乕儖僗儅儞栤戣偱偼丄乽堦昅彂偒乿偲偄偆忦審傪丄乽慡偰偺搒巗偵偍偄偰丄儖乕僩偵娷傑傟傞巬偼昁偢2杮偱偁傞乿偲偄偆忦審偵抲偒姺偊偰庢傝姼偊偢栤戣傪夝偄偰偟傑偆偲偄偆庤朄傪梡偄偰偄傞丅偙偺忦審娚榓偑乽堦昅彂偒乿傪掕幃壔偡傞嵺偺旕忢偵廳梫側億僀儞僩偱偁傞丅偙偺忦審偵抲偒姺偊偨応崌丄慄宍惂栺幃偱昞尰偡傞偙偲偼梕堈偱偁傝丄忋恾偺椺偱偼丄
A : H(A,B)+H(A,C)+H(A,D)+H(A,E)+H(A,F) = 2
B : H(A,B)+H(B,C)+H(B,D)+H(B,E)+H(B,F) = 2
C : H(A,C)+H(B,C)+H(C,D)+H(C,E)+H(C,F) = 2
D : H(A,D)+H(B,D)+H(C,D)+H(D,E)+H(D,F) = 2
E : H(A,E)+H(B,E)+H(C,E)+H(D,E)+H(E,F) = 2
F : H(A,F)+H(B,F)+H(C,F)+H(D,F)+H(E,F) = 2
偺6杮偲側傞丅偙偙偱丄俤倃俠俤俴偺僜儖僶乕偵栚揑娭悢T偲偙偺6杮偺慄宍惂栺幃傪擖椡偡傟偽丄堦扷丄巄掕揑側夝傪媮傔傞偙偲偑偱偒傞丅
栜榑丄偙偺傛偆偵偟偰媮傔偨夝偼傛傝娚偄忦審偱寁嶼偟偨傕偺偱偁偭偨偐傜昁偢偟傕堦昅彂偒偵側傞偲偼尷傜側偄丅乽慡偰偺搒巗偵偍偄偰丄儖乕僩偵娷傑傟傞巬偼昁偢2杮偱偁傞乿偲偄偆忦審偩偲丄恾16偺條偵暋悢偺晹暘弰夞儖乕僩偑宍惉偝傟傞壜擻惈偑偁傞偺偱偁傞丅
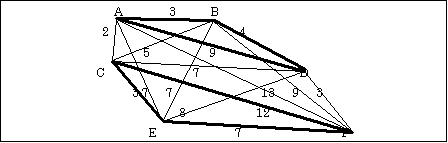
恾16丂乮晹暘弰夞楬乯
弰夞儖乕僩偑1偮偺屌傑傝偵側傜偢丄偙偺傛偆側晹暘弰夞儖乕僩偑夝偵側偭偰偟傑偭偨応崌丄惂栺忦審傪捛壛偟偰嵞寁嶼偡傞昁梫偑偁傞丅晹暘弰夞儖乕僩傪夝徚偡傞偵偼丄晹暘弰夞儖乕僩摨巑傪宷偖偳傟偐偺巬丄懄偪丄AC丄AE丄AF丄BC丄BE丄BF丄CD丄DE丄DF偺壗傟偐偑昁偢儖乕僩偵娷傑傟傞傛偆偵偡傟偽傛偄丅偙傟偼丄H(A,C)+H(A,E)+H(A,F) +H(B,C)+H(B,E)+H(B,F)+H(C,D)+H(D,E)+H(D,F)=亜1偲偄偆慄宍惂栺幃偱昞傢偡偙偲偑偱偒傞丅埥偄偼丄偙偺慄宍惂栺幃偼懢慄儖乕僩傪嬛巭偡傞惂栺丄懄偪丄H(A,B) +H(B,D)+H(A,D)=<2枖偼H(C,E)+ H(C,F)+H(E,F)=<2偱傕傛偄丅
乮曗5拲1偱偦傟偧傟乽晹暘弰夞嬛巭惂栺乿乽晹暘弰夞嫮惂愙懕惂栺乿偲掕媊偟偨丅乯
偙偺傛偆偵丄晹暘弰夞儖乕僩傪夝徚偡傞慄宍惂栺幃傪捛壛偟偰嵞寁嶼傪孞傝曉偟丄媮傔偨儖乕僩偐傜晹暘弰夞儖乕僩偑側偔側傟偽丄偦傟偑媮傔傞堦昅彂偒偺嵟抁儖乕僩偲側傞偺偱偁傞丅
偮傑傝丄乽堦昅彂偒乿偺掕幃壔偼丄嘆乽慡偰偺搒巗偵偍偄偰丄儖乕僩偵娷傑傟傞巬偼昁偢2杮偱偁傞乿偲偄偆忦審傊偺抲偒偐偊丄嘇晹暘弰夞楬偺攔彍丄偵傛偭偰払惉偝傟傞偲偄偆偙偲偱偁傞丅
幚嵺偵偼乽慡偰偺搒巗偵偍偄偰丄儖乕僩偵娷傑傟傞巬偼昁偢2杮偱偁傞乿偲偄偆娚榓忦審偼偐側傝桳岠偱丄偦傟傎偳懡偔偺捛壛忦審傪昁梫偲偟側偄丅偙偺娚榓忦審愝掕偺敪憐偑側偐偭偨傜偍偦傜偔嵟挿曅摴儖乕僩傪媮傔傞偙偲偼憡摉崲擄偵側偭偰偄偨偲巚傢傟傞丅
峏怴婰榐
丂丒丂2005擭6寧21擔丂丗丂乽晹暘弰夞嬛巭惂栺乿乽晹暘弰夞嫮惂愙懕惂栺乿偵偮偄偰偺拲婰捛壛丅
仼慜偺儁乕僕丂栚師丂師偺儁乕僕仺
Copyright(c) 2005丂KONDO Hideaki丂All rights reserved.
弶斉丗 2005擭2寧12擔丂嵟廔峏怴丗 2005擭6寧21擔


