EXCELによる最長片道ルート探索
2. 最長片道ルート問題
巡回セールスマン問題を最長片道ルート問題に適用するのは簡単な類推でできるだろう。まず、都市を分岐駅に、枝を分岐駅間を結ぶ路線に置き換えれば良い。巡回セールスマン問題の枝の数は都市数C2だけあるが、最長片道ルートの枝の数は接続駅数×3〜6しかない。(本州の最長ルート算出では行き止まりの路線については考慮に入れなくても良く、2つなら接続駅とする必要ない。例えば、大宮の枝は大宮-熊谷、大宮-小山、大宮-南浦和、大宮-武蔵浦和、大宮-高麗川の5つ。最高は仙台の6つ。5つも枝があるのは大宮、赤羽、西船橋、品川のみ。)従って、問題がかなり簡略化されることになる。
次に最小化問題を最大化問題にしなければならないが、これは最大化する目的関数にマイナスを掛けたものを最小化すればよい。ちなみにEXCELでは最大化と最小化を選択できるようになっており、目的関数を変更する必要はない。
問題は「全ての都市において、ルートに含まれる枝は必ず2本である」の条件を変更することである。最長片道ルート問題では、最長片道であることが必要であって、必ずしも全接続駅を通らなくてもよい。従って、この条件は「全ての接続駅において、ルートに含まれる枝は2本又は0本である」に変更しなければならない。
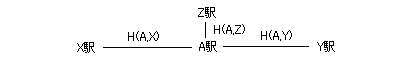
図17
「2本又は0本」の制約を数式で表わすのは意外に難しい。例えば図17のように、枝が3本の場合を考える。なお、表示を簡単にするために、ΣH=H(A,X)+H(A,Y)+H(A,Z)と定義しておく。「2本又は0本」の制約ですぐ思い付くのは、ΣH=2の代わりに制約式を
ΣH×(ΣH−2)=0
とすることである。しかし、これでは(ΣH)2の項が生じるため、制約式が非線型となり、線形計画法で扱えなくなる。EXCELのソルバーでは非線型計画法も実行できるので一応計算は可能であるが、非線形計画法を使う場合、変数が少し増えると、「変数が多すぎて実行できません」というエラーが出てしまうので、結局実用に耐えうるものではなかった。
次に考えたのは、
0=<ΣH/2=<1、ΣH/2=整数
という制約式である。ΣHはもともと整数であるので、0=<ΣH=<2の制約式を設定すれば、ΣHは0、1、2の何れかの値しか取らないことになる。従って、ΣH/2は0、1/2、1の何れかになる。そこで、ΣH/2=整数とすれば、ΣH/2は0と1しかとらないことになるので、ΣHは0または2になることが分かるだろう。ただし、ΣH/2=整数の制約式をEXCELのソルバーに入れようとすると、「整数制約ができるのは変化させるセルだけです」というエラーが発生するので、ダミー変数D(A)を設定し、
0=<ΣH/2=<1、D(A)=整数、D(A)=ΣH/2
という制約式にすることが必要である。この制約式は割合とうまく機能し、本州の名古屋以西の部分は征服できたが、接続駅の数だけ追加のダミー変数が必要なので、枝数と接続駅数の合計が200以上ある東日本地区ではやはり、「変数が多すぎて実行できません」というエラーが出てしまった。(注)EXCELのソルバーで線形計算する場合、変数の設定数の上限は200個である。
それに対し、葛西隆也氏のホームページでは次の制約式を用いていた。
0=<ΣH=<2
−H(A,X)+H(A,Y)+H(A,Z)=>0
H(A,X)−H(A,Y)+H(A,Z)=>0
H(A,X)+H(A,Y)−H(A,Z)=>0
最後の3式は一瞬何のことやら分からないが、ΣH=H(A,X)+H(A,Y)+H(A,Z)に注意すると、
ΣH−2 H(A,X)=>0、 ΣH−2 H(A,Y)=>0、 ΣH−2 H(A,Z)=>0
即ち、
ΣH/2=> H(A,X)、 ΣH/2=> H(A,Y)、 ΣH/2=> H(A,Z)
と同等であることが分かる。つまりΣHを半分にして0〜1の範囲に圧縮し、それを全ての枝の値(それは0又は1である)と比較する。すると、ΣH/2が1/2になった時は、H(A,X)、H(A,Y)、H(A,Z)のどれかが1であるので、ΣH/2=> 1が成立しなくなり、ΣH=1のケースが排除されるのである。ΣH/2を直接0,1と比較するのではなく、H(A,X)、H(A,Y)、H(A,Z)と比較する所がミソである。
上記は接続駅の枝が3本の場合であるが、この定式化は、接続駅の枝数が増えても応用はとても簡単で、例えば枝が5本の時はΣH/2と比較する枝を5本にするだけのことである。この方式は制約式数が接続駅×各枝数で急速に増加するが、変数を増加させる必要がないので、EXCELのソルバーでも計算を開始させることができた。ただし、この計算も非常に時間が掛かるので、実用上は、もう少し条件を緩和してやる必要がある。実は0=<ΣH=<2とだけした場合、実際にはほとんどの接続駅でΣH=2となるため、予め全接続駅の全ての枝に対してこの制約式を課す必要はないのである。色々試してみたが、接続駅の枝数は3本のことが多いので、全接続駅に対して3本のみこの制約式を課し、その上でΣH=1となった接続駅のみに対して、全ての枝に対する制約式を追加した再計算を行うこととした。この方法を採用したところ、全ての枝に対して最後の式を追加する必要のある接続駅は2〜3駅程度となり、制約式をかなり減らすことができた。
また、必ずしも全接続駅を通らなくてもよいという性質は、部分巡回ルートの回避においても若干の影響をもたらす。全接続駅を通るならば、部分巡回ルート同士を繋ぐどれかの枝が必ずルートに含まれなければならないが、通らないという選択枝があるならば、部分巡回ルート全てを放棄することも可能だからである。したがって「部分巡回ルート同士を繋ぐどれかの枝を必ず通る」という制約を使った場合は、部分巡回ルートを放棄するケースについても検討が必要である。もう1つの方法である「部分巡回禁止制約」を使うのであれば、最長片道ルート問題に適用するにあたって特に変更は必要ない。
(補5注1で、「部分巡回ルート同士を繋ぐどれかの枝を必ず通る」という制約を「部分巡回強制接続制約」と定義した。)
更新記録
・ 2005年4月30日 : EXCELソルバーの変数の設定数について誤記訂正。
・ 2005年6月21日 : 「部分巡回禁止制約」「部分巡回強制接続制約」についての注記追加。
←前のページ 目次 次のページ→
Copyright(c) 2005 KONDO Hideaki All rights reserved.
初版: 2005年2月12日 最終更新: 2005年6月21日