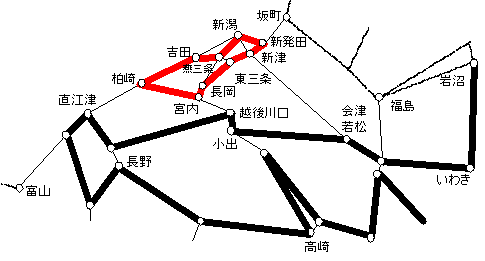
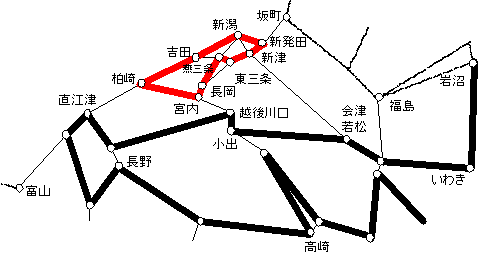
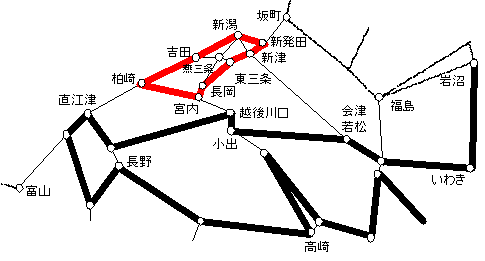
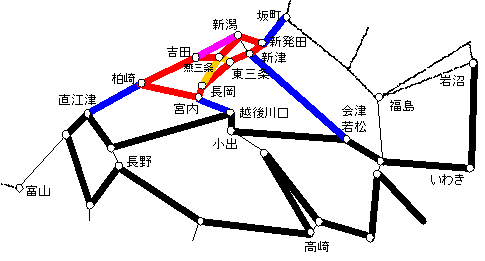
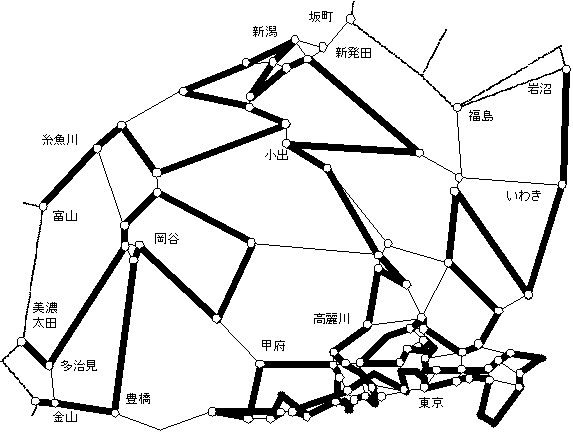
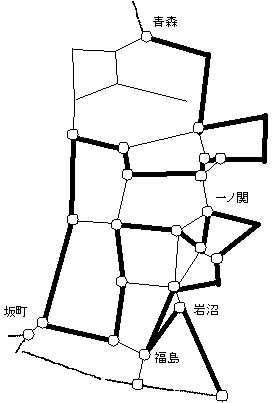
乽偦偺1丗惍悢惂栺傪娚榓乿偱偼丄20暘掱搙偺寁嶼傪4暘掱搙偵抁弅偡傞偙偲偑偱偒偨丅乽偦偺2乿偱偼丄乽偦偺1乿偲偼堎側傞傾僾儘乕僠偲側傞乽儔僌儔儞僕儏娚榓乿傪梡偄傞曽朄傪専摙偡傞丅儀儞僠儅乕僋偡傞椺戣偼乽偦偺1乿偲摨偠偱偁傞丅
寢榑偐傜尵偆偲丄乽儔僌儔儞僕儏娚榓乿偱偼20暘掱搙偺寁嶼傪10暘掱搙偵抁弅偡傞偙偲偑偱偒偨偑丄乽儔僌儔儞僕儏娚榓乿偐傜偺巚偄偮偒偱帋傒偨乽嬌傔偰娙扨側曽朄乿偵傛傝丄20暘掱搙偺寁嶼傪側傫偲1暘掱搙偵抁弅偡傞偙偲偑偱偒偨丅偙傟偼丄乽偦偺1乿偺惉壥傪偼傞偐偵忋夞傞傕偺偱偁傞丅
乽嬌傔偰娙扨側曽朄乿偲偼丄晹暘弰夞儖乕僩偑敪惗偟偨応崌偵丄乽晹暘弰夞嬛巭惂栺乮晹暘弰夞儖乕僩忋偱巊梡偱偒傞巬悢亙亖晹暘弰夞儖乕僩偺慡巬悢亅1乯乿偱偼側偔丄乽晹暘弰夞嫮惂愙懕惂栺乿傪巊梡偟丄偐偮丄乽晹暘弰夞嫮惂愙懕惂栺乿傪乽晹暘弰夞儖乕僩偐傜撍偒弌偟偨巬偺偆偪捠夁偡傞杮悢亜亖1乿偱偼側偔丄乽晹暘弰夞儖乕僩偐傜撍偒弌偟偨巬偺偆偪捠夁偡傞杮悢亜亖2乿偲偡傞偙偲偱偁傞
乮拲1嶲徠乯丅
柺敀偄偺偼丄乽晹暘弰夞嬛巭惂栺乿偱偼側偔丄乽晹暘弰夞嫮惂愙懕惂栺乿傪巊梡偟偨応崌丄乽晹暘弰夞儖乕僩偐傜撍偒弌偟偨巬偺偆偪捠夁偡傞杮悢亜亖1乿偱傕丄寁嶼帪娫偼6暘掱搙偵抁弅偝傟傞偺偱偁傞偑丄1傪2偵曄偊傞偩偗偱丄寁嶼帪娫偑峏偵戝暆抁弅偝傟丄1暘掱搙偵側傞偙偲偱偁傞丅
晹暘弰夞儖乕僩偑敪惗偟偨応崌偵乽晹暘弰夞嫮惂愙懕惂栺乿傪梡偄傞偙偲偼丄
弰夞僙乕儖僗儅儞栤戣偱傕婛弌偱偁傞偐傜丄偙傟傪梡偄傞曽偑丄寁嶼偑懍偔側傞偙偲偵崱傑偱婥偑晅偐側偐偭偨偺偑晄巚媍側偔傜偄偱偁傞偑丄側偤偙偺曽朄偺曽偑丄寁嶼偑懍偄偺偐偼丄偼偭偒傝偲偼暘偐偭偰偄側偄丅崱夞偼丄怴偨側暘婒曄悢偺敪惗傪偱偒傞偩偗尭傜偡偲偄偆曽岦惈偱専摙偡傞偆偪偵丄乽晹暘弰夞嫮惂愙懕惂栺乿偺妶梡傪嵞敪尒偡傞偵帄偭偨偑丄偙偺曽朄偵扝傝拝偒偔傑偱偺榖偺嬝傪埲壓偵弎傋傞偙偲偱丄偙偺嵞敪尒偺堄媊傪柧傜偐偵偟偨偄丅
偄偢傟偵偟偰傕寁嶼帪娫1暘掱搙偼丄偐側傝枮懌偱偒傞儗儀儖偱偁傞丅崱屻偺僜儖僶乕偱偺寁嶼偼丄乽晹暘弰夞嬛巭惂栺乿傛傝傕乽晹暘弰夞嫮惂愙懕惂栺乿傪梡偄傞偙偲傪悇彠偟偨偄丅
亂昞A5-8亃
| 乮嶉嬍導丗1杮乯 |
|---|
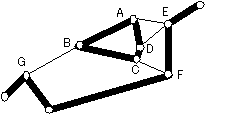
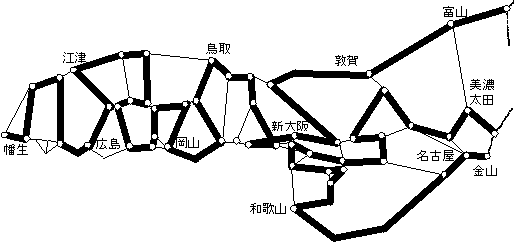
- H(戝媨,孎扟)亄H(孎扟,憅夑栰)亄H(憅夑栰,崅楉愳)亄H(崅楉愳, 戝媨)亙亖3
|
|
|
| 乮朳憤敿搰丗3杮乯 |
|---|
- H(搶嫗,昳愳)亄H(搶嫗,恄揷)亄H(廐梩尨,嬔巺挰)亄H(惣慏嫶,怴徏屗)亄H(変懛巕,惉揷)亜亖2
|
- H(昳愳,愳嶈)亄H(昳愳,掃尒)亄H(昳愳,怴墶昹)亄H(戙乆栘,怴廻)亄H(廐梩尨,擔曢棦)亄H(惣慏嫶,怴徏屗)亄H(変懛巕,惉揷)亜亖2
|
- H(搶嫗,昳愳)亄H(昳愳,戙乆栘)亄H(惣崙暘帥,晎拞杮挰)亄H(惣崙暘帥,棫愳)亄H(晲憼塝榓,戝媨)亄H(晲憼塝榓,撿塝榓)亄H(撿塝榓,愒塇)亄H(擔曢棦,怴徏屗)亄H(惣慏嫶,怴徏屗)亄H(変懛巕,惉揷)亜亖2
|
| 乮怴妰嬤峹丗1杮乯 |
|---|
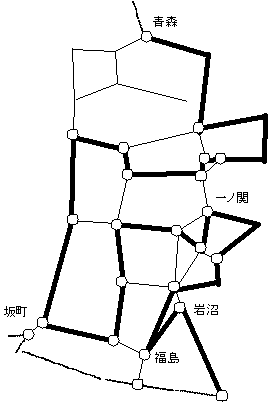
- H(攼嶈,捈峕捗)亄H(媨撪,墇屻愳岥)亄H(怴捗,夛捗庒徏)亜亖2
|
| 乮搶奀抧曽-杮廈弞娐宆嵟挿曅摴儖乕僩偱巊梡偟偨傕偺丗4杮乯 |
|---|
|
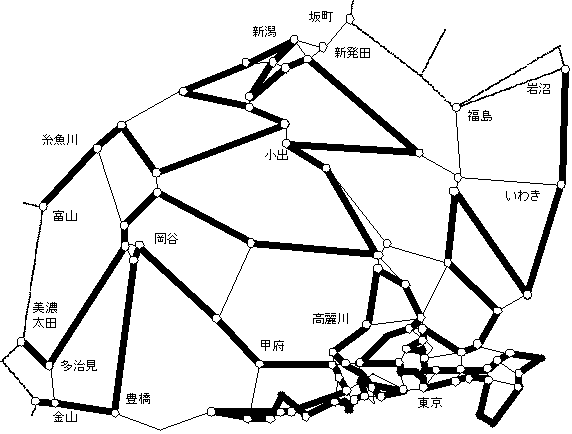
- H(朙嫶,惷壀)亄H(壀扟,彫暎戲)亄H(墫怟,徏杮)亜亖2
|
- H(朙嫶,惷壀)亄H(彫暎戲,峛晎)亄H(攓搰,崅楉愳)亄H(惣崙暘帥,棫愳)亄H(惣崙暘帥,晎拞杮挰)亄H(昳愳,怴墶昹)亄H(昳愳,愳嶈)亄H(昳愳,掃尒)亜亖2
|
- H(朙嫶,惷壀)亄H(彫暎戲,峛晎)亄H(攓搰,崅楉愳)亄H(惣崙暘帥,棫愳)亄H(惣崙暘帥,晎拞杮挰)亄H(昳愳,戙乆栘)亄H(昳愳,搶嫗)亜亖2
| 乮捛壛丗5杮乯 |
|---|
- H(巺嫑愳,捈峕捗)亄H(挿栰,朙栰)亄H(彫弌,墇屻搾戲)亄H(夛捗庒徏,孲嶳)亜亖2
|
- H(巺嫑愳,徏杮)亄H(挿栰,朙栰)亄H(彫弌,墇屻搾戲)亄H(埨愊塱惙,孲嶳) 亄H(偄傢偒,悈屗)亜亖2
|
- H(偄傢偒,悈屗)亄H(埨愊塱惙,孲嶳)亄H(彫弌,墇屻搾戲)亄H(崅嶈,嵅媣)亄H(峛晎,彫暎戲)亄H(朙嫶,惷壀)亜亖2
|
- H(巺嫑愳,捈峕捗)亄H(挿栰,朙栰)亄H(彫弌,墇屻愳岥)亄H(夛捗庒徏,怴捗)亜亖2
|
- H(巺嫑愳,徏杮)亄H(挿栰,朙栰)亄H(崅嶈,嵅媣)亄H(峛晎,彫暎戲)亄H(朙嫶,惷壀)亜亖2
|
|
亂昞A5-9亃
| 乮嶉嬍導丗1杮乯 |
|---|
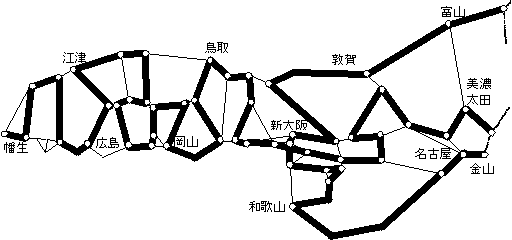
- H(戝媨,孎扟)亄H(孎扟,憅夑栰)亄H(憅夑栰,崅楉愳)亄H(崅楉愳, 戝媨)亙亖3
|
|
|
| 乮朳憤敿搰丗3杮乯 |
|---|
- H(搶嫗,昳愳)亄H(搶嫗,恄揷)亄H(廐梩尨,嬔巺挰)亄H(惣慏嫶,怴徏屗)亄H(変懛巕,惉揷)亜亖2
|
- H(昳愳,愳嶈)亄H(昳愳,掃尒)亄H(昳愳,怴墶昹)亄H(戙乆栘,怴廻)亄H(廐梩尨,擔曢棦)亄H(惣慏嫶,怴徏屗)亄H(変懛巕,惉揷)亜亖2
|
- H(搶嫗,昳愳)亄H(昳愳,戙乆栘)亄H(惣崙暘帥,晎拞杮挰)亄H(惣崙暘帥,棫愳)亄H(晲憼塝榓,戝媨)亄H(晲憼塝榓,撿塝榓)亄H(撿塝榓,愒塇)亄H(擔曢棦,怴徏屗)亄H(惣慏嫶,怴徏屗)亄H(変懛巕,惉揷)亜亖2
|
| 乮怴妰嬤峹丗1杮乯 |
|---|
- H(攼嶈,捈峕捗)亄H(媨撪,墇屻愳岥)亄H(怴捗,夛捗庒徏)亜亖2
|
| 乮搶奀抧曽-杮廈弞娐宆嵟挿曅摴儖乕僩偱巊梡偟偨傕偺偺撪丄屻敿2杮乯 |
|---|
- H(朙嫶,惷壀)亄H(彫暎戲,峛晎)亄H(攓搰,崅楉愳)亄H(惣崙暘帥,棫愳)亄H(惣崙暘帥,晎拞杮挰)亄H(昳愳,怴墶昹)亄H(昳愳,愳嶈)亄H(昳愳,掃尒)亜亖2
|
- H(朙嫶,惷壀)亄H(彫暎戲,峛晎)亄H(攓搰,崅楉愳)亄H(惣崙暘帥,棫愳)亄H(惣崙暘帥,晎拞杮挰)亄H(昳愳,戙乆栘)亄H(昳愳,搶嫗)亜亖2
| 乮捛壛丗3杮乯 |
|---|
- H(巺嫑愳,捈峕捗)亄H(挿栰,朙栰)亄H(彫弌,墇屻搾戲)亄H(夛捗庒徏,孲嶳)亜亖2
|
- H(偄傢偒,悈屗)亄H(埨愊塱惙,孲嶳)亄H(彫弌,墇屻搾戲)亄H(崅嶈,嵅媣)亄H(峛晎,彫暎戲)亄H(朙嫶,惷壀)亜亖2
|
- H(巺嫑愳,捈峕捗)亄H(挿栰,朙栰)亄H(彫弌,墇屻愳岥)亄H(夛捗庒徏,怴捗)亜亖2
|
|