恾A4-1
乽俤倃俠俤俴偵傛傞嵟挿曅摴儖乕僩扵嶕乿4乮1乯怴姴慄傪娷傓捠忢偺嵟挿曅摴儖乕僩偱弎傋偨傛偆偵丄杮廈抧嬫偺嵟挿曅摴儖乕僩偼丄俤倃俠俤俴偺僜儖僶乕傪梡偄偰寁嶼偡傞応崌丄僜儖僶乕偺曄悢愝掕偺忋尷側偳偵傛傝暘妱寁嶼傪偣偞傞傪摼側偄丅偦偺忋丄娭搶傪娷傓搶擔杮抧曽偵偮偄偰偼丄1夞偺寁嶼偱嵟戝20暘掱搙偺帪娫偑妡偐偭偰偍傝丄傑偩傞偭偙偟偄丅偙偺傛偆側忬懺偱偼丄乽側傫偲偐丄偓傝偓傝偺偲偙傠偱寁嶼偱偒偰偄傞乿偲偄偆儗儀儖偲尵傢偞傞傪偊側偄丅
俤倃俠俤俴偺僜儖僶乕傪梡偄傞埲忋丄暘妱寁嶼偼傗傓傪摼側偄偑丄搶擔杮抧曽偺寁嶼偼側傫偲偐崅懍壔傪恾傝偨偄丅
偦偙偱丄崱夞丄偄傠偄傠偲帋偟偨偲偙傠丄堭偯傞幃偵寁嶼崅懍壔偵岠壥揑側庤朄偑尒偮偐傝丄乽偦偺1乿偺惉壥偲偟偰偼丄20暘掱搙偺寁嶼傪4暘掱搙偵抁弅偡傞偙偲偑偱偒偨丅
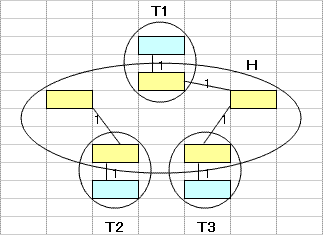
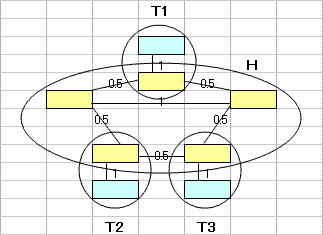
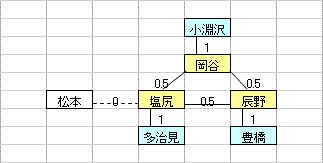
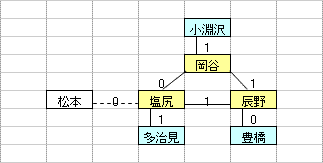
乽偦偺1乿偼丄墂娫偺巬偵愝掕偟偨0,1曄悢H(m,n)偺乽惍悢惂栺傪娚榓乿偡傞偙偲偵傛偭偰丄寁嶼懍搙傪岦忋偝偣傞傕偺偱偁傞丅惂栺娚榓偺曽朄偲偟偰偼丄懠偵乽儔僌儔儞僕儏娚榓乿傪梡偄傞曽朄傕峫偊傜傟丄偙偪傜偼丄乽偦偺2乿偱専摙偡傞偙偲偲偟偨丅
乽偦偺1乿偺庤朄偼丄傑偩丄惂栺幃乮摿偵丄乽愙懕墂偵偍偄偰儖乕僩偵娷傑傟傞巬偼0杮傑偨偼2杮乿偺惂栺乯偵夵慞偺梋抧偑偁傞偲巚傢傟傞丅抦尒偺偁傞撉幰偺曽偑嫃傜傟偨傜丄惀旕丄夵慞曽朄傪嫵帵捀偒偨偄丅

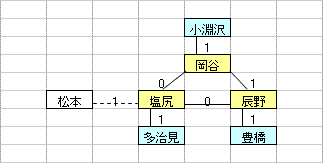
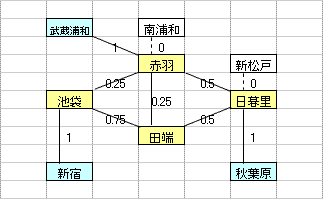
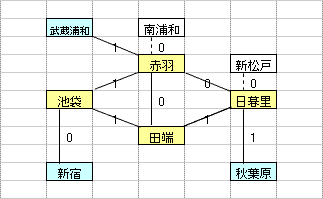
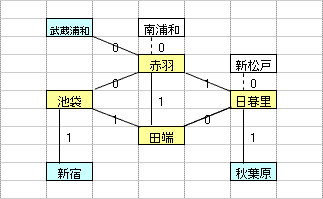
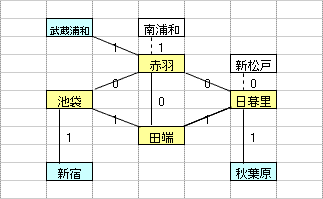
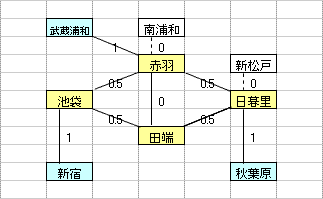
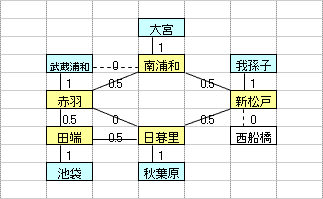
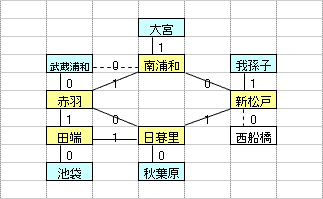
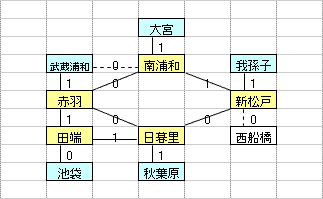
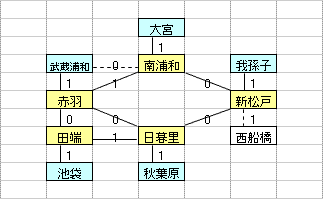
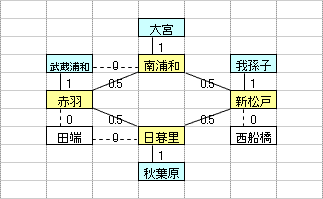
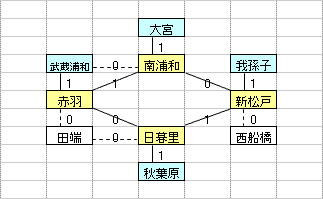
| 乮孂惂栺丗6屄乯 |
|---|
|
|
|
|
|
|
| 乮惍悢惂栺丗14屄乯 |
| 丂丂丒丂H(朙嫶,扖栰)亖惍悢 |
| 丂丂丒丂H(彫弌,夛捗庒徏) 亖惍悢 |
| 丂丂丒丂H(夛捗庒徏,怴捗) 亖惍悢 |
| 丂丂丒丂H(彫暎戲,嵅媣)亖惍悢 |
| 丂丂丒丂H(彫暎戲,壀扟) 亖惍悢 |
| 丂丂丒丂H(搶恄撧愳,姖儢嶈) 亖惍悢 |
| 丂丂丒丂H(怴妰,媑揷) 亖惍悢 |
| 丂丂丒丂H(変懛巕,惉揷)亖惍悢 |
| 丂丂丒丂H(怴敪揷,怴妰) 亖惍悢 |
| 丂丂丒丂H(怴捗,搶嶰忦) 亖惍悢 |
| 丂丂丒丂H(挿壀,墠嶰忦) 亖惍悢 |
| 丂丂丒丂H(惣慏嫶,愮梩)亖惍悢 |
| 丂丂丒丂H(昳愳,愳嶈) 亖惍悢 |
| 丂丂丒丂H(屼拑僲悈,戙乆栘) 亖惍悢 |